Introducción

Conceptos

Epidemia: Es el aumento de la incidencia de casos similares en poblaciones humanas en un área geográfica determinada. Y constituyen el mayor punto de interés para la epidemiología.

Epidemiologia: Se define como el estudio de la distribución, frecuencia y determinantes del proceso salud-enfermedad en poblaciones humanas. Es una disciplina científica dedicada al estudio de los determinantes, la distribución, la frecuencia, las predicciones y el control de los factores vinculados a la salud y la enfermedad de los seres humanos. De esta manera intenta determinar la relación de causa y efecto entre la exposición y la enfermedad. Utiliza recursos de las ciencias de la salud, como la medicina y de las ciencias sociales para estudiar el bienestar de las personas de una comunidad determinada.

Epidemiología matemática: Es un campo multidisciplinario que utiliza técnicas de temas clásicos de la ciencia de la computación, matemáticas, la ciencia de la información geográfica y la salud pública. Las cuales ayudan a desarrollar modelos matemáticos que describe el comportamiento observado de los virus, en base a los datos disponibles. Para luego, realizar simulaciones del modelo para comprender los posibles resultados dado el modelo utilizado. Analiza cómo ocurren las epidemias en poblaciones y en hospitales, y cómo éstas se pueden controlar, por lo que podemos poner énfasis en que personas podemos monitorear, a quién vacunar, cuándo vacunar, cómo identificar a los grupos de riesgo y cómo saber cuándo aislarlos, etc.

Historia de las epidemias

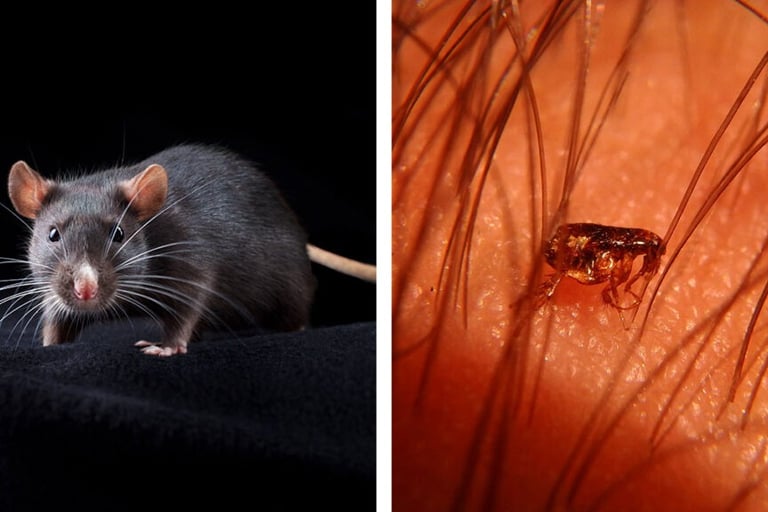
A lo largo de la historia de la humanidad, el hombre ha sufrido diversas enfermedades las cuales se extendieron produciendo epidemias y pandemias dejando un gran número de muertos. Estas epidemias y pandemias eran conocidas en la antigüedad como plagas o pestes. Y los primeros antecedentes consideraban que las plagas se propiciaban debido a los hábitos personales, al medio ambiente que los rodea, en particular ´el consideraba a las estaciones cálidas y húmedas como los lugares propicios para el desarrollo de una enfermedad.

Ejemplo de esto tenemos la epidemia más devastadora de la historia de la humanidad, la peste negra, la cual terminó con la vida de entre 75 y 200 millones de personas en el siglo XIV. El brote repentino de esta enfermedad afectó, según estiman modelos de predicción actuales, a entre 75 y 200 millones de personas, que traducido a porcentaje, se encuentra entre un 30 y un 60 por ciento de la población total de Europa.

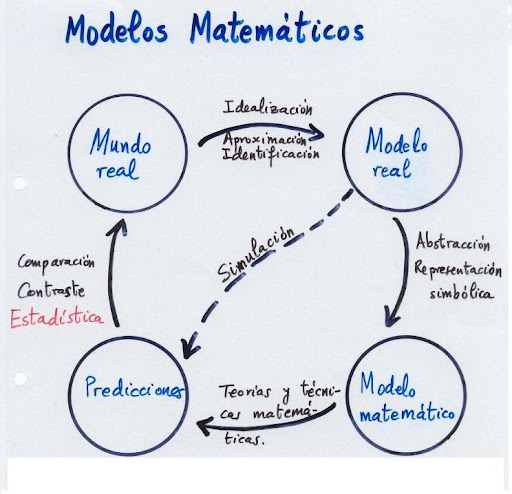
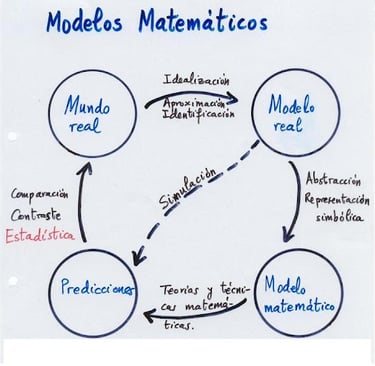
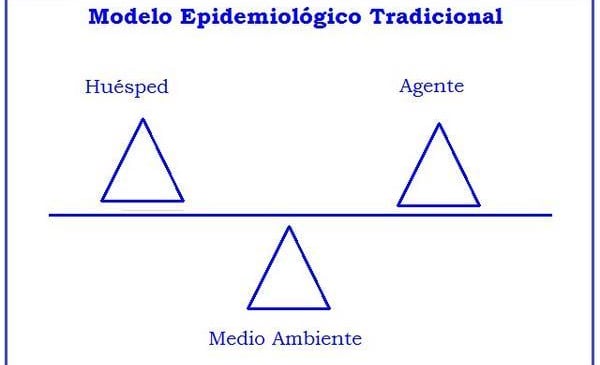
Los modelos en diferentes disciplinas

Las epidemias no solo se enfocan en temas sanitarios, también se relacionan con fenómenos socio económicos y las dinámicas de otros sectores como el turismo o la agricultura, por tanto, debemos tener una visión sistémica. Además de los avances que se han acelerado por la pandemia COVID-19, discutimos sobre las oportunidades y retos para luchar epidemias de manera más eficaz y humana en ramas como la economía, como socializa las personas, y desarrollo personal.

Importancia de modelos matemáticos

El objetivo de los modelos matemáticos es obtener y analizar los datos observados para avanzar hacia la comprensión del comportamiento del sistema, y poder predecir el comportamiento epidemiológico y evaluar las posibles estrategias de control.

La construcción de modelos matemáticos es una de las herramientas utilizadas hoy en día para el estudio de problemas en medicina, biología, fisiología, bioquímica, epidemiología, fármaco-cinética, entre otras áreas del conocimiento.

Cabe destacar que los modelos matemáticos en el campo de la epidemiología computacional se utilizan como herramienta para tomar decisiones y que deben valorarse, ya que difícilmente es comprensible un problema complejo sin una mínima modelación o alguna idea de esta, aunque también hay que reconocer que no es posible modelar la totalidad de las situaciones reales.

En esencia, la función central de crear y analizar modelos matemáticos es mejorar la comprensión de un sistema para prevenir futuras situaciones de enfermedades, determinar la prevalencia e incidencia y coadyuvar a tomar decisiones objetivas para controlar o erradicar las enfermedades. Muchas veces es importante resaltar que un modelo matemático está definido por relaciones. Relaciones que son independientes de los datos a introducir en el modelo, ya que un modelo puede usarse para diferentes ocasiones y en distintos contextos.

---- Limitación ----

Sin embargo, su aplicación se ve limitada por la falta de conocimientos e información acerca de los principios básicos del modelamiento matemático. Ejemplo de esto es:

1. La construcción de modelos revela algunas veces relaciones que no son obvias a primera vista.

2. Ya construido el modelo matemático no siempre es posible extraer de él propiedades y características de las relaciones entre los elementos que de otra forma permanecerían ocultas.

3. Obtener los datos está siendo uno de los retos más importantes en esta crisis, desde la falta de un sistema unificado de adquisición de datos y de sistemas de información hasta la dificultad de publicarlos han sido y son dificultades importantes.

------Dentro de la epidemiología computacional-----

Dentro de la epidemiologia computacional se utilizan de forma casi generalizada modelos estructurados en compartimentos (SIR, SEIR, ...), basados en las relaciones desde la perspectiva epidemiológica entre personas susceptibles y personas infecciosas. Estos modelos pueden ser simples o pueden llegar a ser muy complejos.

La relación entre el número de personas susceptibles y el número de personas infecciosas en ningún momento ha sido determinante para definir el rumbo de alguna pandemia, sino que el comportamiento epidemiológico ha sido determinado por las medidas de control, donde encontramos: confinamientos domiciliarios, limitación de movilidad, etc.

---- Proceso de trabajo de los modelos epidemiológicos ----

1.Previo a la epidemia:

Desarrollo de protocolos de actuación Evaluación de las necesidades de salud: Personal de salud (médicos, enfermeras …), camas hospitalarias, UCI, equipo médico.

• Durante la epidemia:

Obtención de información básica propia del país Proyección de casos (núm. de casos, distribución geográfica, diseminación)

Evaluación de la efectividad de las medidas de control

• Posterior a la epidemia:

Vigilancia epidemiológica

Por otra parte, la falta de conocimientos de una enfermedad nueva y de información de algunos parámetros hacía imposible calibrar los modelos, desde los más simples a los más complejos. A pesar de estas limitaciones, otro tipo de modelos permitieron hacer previsiones: los modelos empíricos. Modelos basados en el análisis de series temporales con métodos más o menos sofisticados, desde modelos clásicos de la demografía hasta herramientas de la inteligencia artificial. 

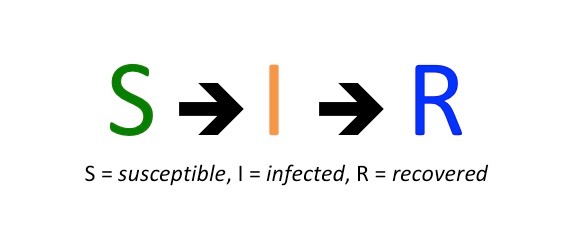
Modelo 𝑆𝐼𝑅

El modelo 𝑆𝐼𝑅 formulado en 1927 por Kermack-McKendrick es un modelo de compartimentos donde la población bajo estudio se divide en clases epidemiológicas y se describe un flujo entre ellas. Y se basa en un sistema ecuaciones diferenciales, las que constituyen una herramienta fundamental en la modelización de procesos biológicos mediante variables y parámetros.

Un modelo centrado en estados donde lo importante es la variación de éstos a lo largo del tiempo, así que dividiremos a la población de individuos atacados por el virus en tres clases.

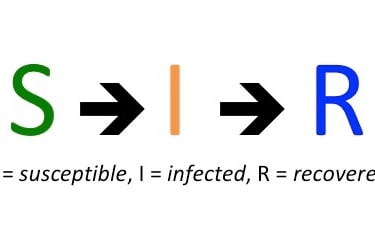
1. Susceptibles (𝑺): Individuos sanos de la población que pueden contraer la enfermedad.

2. Infectados (𝑰): Individuos infectados y que pueden contagiar a otros.

3. Recuperados (𝑹): Individuos resistentes a la enfermedad, normalmente la han superado o han sido vacunados.

Aunque, se puede pasar de un grupo a otro, aunque solo en una dirección, como se muestra en el siguiente esquema:

𝑺 → 𝑰 → 𝑹

Por tanto, un miembro 𝑺, puede contagiar (pasar de 𝑺 a 𝑰) y uno 𝑰 se puede recuperar (pasar de 𝑰 a 𝑹) o puede morir. En este modelo se supone que la recuperación proporciona inmunidad y no se regresa al grupo 𝑺. Y las personas que fallecen por la enfermedad se incluyen también en el grupo 𝑹, con lo que la población total se mantiene constante.

Veamos que hay una simplificación en el modelo, ya que no tiene en cuenta ni los nacimientos ni las muertes por otros motivos. Aunque, existen modelos más complejos que también contemplan esos casos.

---- Sistema de ecuaciones ----

Sea t la variable que indica el tiempo y 𝑺(t), 𝑰(t) y 𝑹(t) el número de personas que hay en cada grupo en un momento t determinado.

Y sea N el tamaño de la población, es decir:

𝑺(t) + 𝑰(t) + 𝑹(t) = N, para todo t.

Este modelo asume que la población total N se mantiene constante en el tiempo, o sea, es la suma de los susceptibles más los infectados más los recuperados.

Para plantear las ecuaciones, es necesario formular la velocidad de cambio de esas tres funciones. La expresión matemática de la velocidad es una derivada. He aquí las ecuaciones del modelo SIR:

Dado que el riesgo de contagio depende de los contactos entre miembros de los grupos S e I, la hipótesis del modelo SIR es que sus encuentros son proporcionales al producto de S por I.

Además el factor "tasa de transmisión" debe multiplicarse por dicho producto para calcular la velocidad de cambio del grupo susceptible. Tasa que expresamos como: a/N.

El término expresa la velocidad con que se pasa de S a I. Dado que en el proceso el n.º de susceptibles disminuye y el de personas infectadas aumenta, es negativo para S’ y positivo, en cambio, para I’.

Por otra parte, quienes se curen o fallezcan pasarán de I a R. Para calcular cuántas personas lo hacen tenemos la tasa de recuperación, que ha de multiplicarse por el número de personas infectadas. Por eso aparece el término en las ecuaciones; es negativo para I’, porque reduce el n.º de personas infectadas y positivo para R’, porque hacer aumentar el n.º de recuperadas.

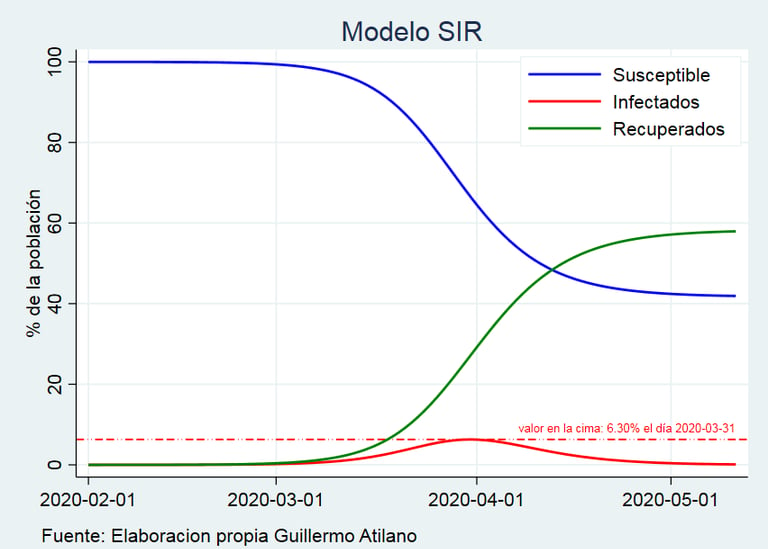
Podemos ver que el valor I(t) tiende a 0 según avanza el tiempo, es decir, se reduce el n.º de personas infectadas. Viendo los datos reales no se percibe la existencia de este umbral, por lo que el modelo matemático fue esencial para llegar a esa conclusión.

Por otro lado, la función I(t) llega a un valor máximo y luego comienza a descender, sin incrementarse de nuevo. Es decir, tiene un único pico. Esta es otra de las propiedades que revela el modelo matemático.

De esta manera vemos que el modelo es muy simple pero a veces la realidad puede ser distinta.

Los modelos epidemiológicos sin duda son una herramienta de gran importancia para poder explicar el comportamiento y la afectación de ciertas enfermedades en diferentes momentos de la historia ya que nos permiten obtener información relevante del cómo poder actuar en el futuro y cómo implementar estrategias eficaces de contención.

Referencias 

• https://www.scielosp.org/article/rcsp/2020.v46suppl1/e2597/ https://www.scielosp.org/pdf/spm/2007.v49n3/218-226/es

• https://www.fcfm.buap.mx/assets/docs/docencia/tesis/matematicas/EmileneCarmelitaPliegoPliego.pdf

• https://culturacientifica.com/2020/08/24/el-modelo-sir-un-enfoque-matematico-de-la-propagacion-de-infecciones/ http://www.criiasupr.org/multimedia/documents/Modelos%20Puerto%20Rico%20varios-Dr.%20Juan%20Carlos%20Orengo.pdf

• Álvarez, C., Andrade, E. & Gauthier, V. (2015). Modelos epidemiológicos en redes: una presentación introductoria. Boletín de Matemáticas, 22(1), 21–37. https://revistas.unal.edu.co/index.php/bolma/article/view/51844

• Rodríguez, R. (2015). La reinvención de la epidemiología a la luz de las nuevas tecnologías. Revista Ciencias de la Salud, 13(2), 283-291.https://doi.org/10.12804/revsalud13.02.2015.13