MATEMÚSICA: Pitágoras y su grandioso descubrimiento musical

Todos tenemos un instinto matemático, de la manera más intuitiva podemos poner como ejemplo el realizar una medición, así es, probablemente tengas un recuerdo en el cual para medir algo utilizaste tu ingenio; con tus manos, tus brazos o tratando de imaginarte otros objetos trataste de comparar los tamaños, formas y espacios. Algo que podría parecernos un método improvisado y poco confiable para comparar dimensiones o cantidades, es de hecho la forma empírica en la que se empezó a realizar esta tarea.

Hoy en día ya tenemos un método de comparación definido dependiendo de lo que queramos medir, pero en la antigüedad era muy poco común el uso de las escalas, el uso de la intuición era la única herramienta para hacer mediciones a través de la comparación, no sabemos con exactitud quién determinó cómo se debía comparar con qué, pero seguramente es gracias a estas situaciones de prueba y error que nuestra vida es más fácil. En este sentido hay algo que requiere también del uso de una métrica, la música. Sin la comprensión y el uso adecuado de la métrica sería difícil componer melodías, he ahí que el día de hoy hablaremos de uno de los casos más antiguos dentro de la historia de la composición musical. El caso de Pitágoras y la música.

¿Música y composición? Pitágoras y la leyenda de los yunques

Durante el siglo VI a.C. surgen algunos conceptos que exploraremos y nos van a introducir a un viaje muy interesante a través de la música. Pero antes de tecnicismos, vale la pena hacer una reflexión personal, ¿Qué es la música?, ¿Qué podemos considerar como música? Independientemente de nuestra respuesta, es claro que para intentar hacer música es necesario producir sonido y es probable que más de uno se esté preguntando ¿Cómo podemos manipular el sonido?

De la misma forma en que hacemos una receta de cocina o seguimos un instructivo para ensamblar un objeto, nos gustaría tener las medidas exactas y los ingredientes necesarios para crear una pieza musical. El problema es que es un tanto complicado medir el sonido ‘a ojo de buen cubero’. El sonido se mide en decibeles, la cual utiliza una escala logarítmica y para calcular su intensidad tenemos que considerar factores como la presión y el aire como el medio en el cual se transmitirán las ondas producidas por la vibración de un objeto o fuente.

En este contexto y como si se tratara de una máquina creada por un artesano, los primeros conocimientos formales en la música occidental fueron formados en una herrería, fue en este lugar donde un matemático griego llamado Pitágoras se dio cuenta de que los martillos utilizados en la herrería provocan diferentes sonidos al ser golpeados. Heller-Roazen (2011) cuenta que Pitágoras estaba buscando la forma de estudiar las propiedades del sonido sin preocuparse de la forma que tenían los objetos que emitían estos estudiando sus propiedades únicamente a través de la razón. Cuando Pitágoras se dio cuenta de que la diferencia de los sonidos no era causada ni por la fuerza con la que se golpeaban, ni por el material por el que estaban hechos, sino más bien es el peso de estos, fue en ese momento que pudo guiar su investigación al terreno que él deseaba.

Pitágoras, la leyenda

Pitágoras fue un filósofo y matemático cuyo nacimiento suele ser situado en el siglo VI antes de Cristo, alrededor del año 570 a.C., en una isla griega llamada Samus. Se dice que dejó su tierra natal para trasladarse a la Magna Grecia alrededor del año 530 a.C. Algo curioso de este personaje es que algunos detalles de su vida se contradicen, podríamos decir que queda más su leyenda que un registro fidedigno de su vida. Pitágoras fue una persona de mucha influencia en todos los ámbitos intelectuales, incluso tuvo una gran cantidad de seguidores que se hacían llamar Los Pitagóricos, más que una escuela era una sociedad secreta que tenía ideas científicas y propias creencias casi religiosas, eran un grupo de personas que se identificaban por un símbolo (como si se tratara del logotipo de una banda) y que tenían la creencia de que a todas las cosas en el mundo se les podía asociar un número.

Regresando a la leyenda de los yunques…

Pitágoras fue una persona a la que se le reconoció como alguien sabio, de hecho, hasta nuestros días se ha discutido bastante sobre la influencia que ha tenido en otros pensadores de su época, en el libro “The musical structure of Plato's dialogue” el autor J. B. Kennedy asegura que al momento de redactar sus diálogos, Platón dividió en renglones y párrafos de tal forma que buscara una musicalidad parecida a la de las escalas pitagóricas con las que al igual que en las composiciones se le quiso dar una harmonía como a las quintas y a las octavas que definía Pitágoras.

¿Tonos?, ¿octavas?, qué es lo que Pitágoras nos trataba de decir con estos enunciados que pueden parecernos tan complicados.

Para responder estas preguntas hay que regresar a la historia en la que Pitágoras escuchaba el estruendo de los martillos al pasar junto a una herrería. Él estaba impresionado por la diferencia de sonidos que estos presentaban, debido a que Pitágoras creía que a todo se le podía asociar un número es probable que se haya aventurado a tratar de medir el sonido, tratando de dar una explicación al fenómeno de los diferentes sonidos pensó en posibles explicaciones: el material con el que estaban hechos los martillos, el grosor de estos, el aire en el ambiente y hasta pensó en la fuerza con la que estos eran golpeados.

Pitágoras se dio cuenta de que la verdadera razón por la que los martillos sonaran de forma diferente se debía al peso de estos, al comparar sus pesos se dio cuenta que existía una relación interesante, al compararlos uno resultaba tener el doble del peso que el otro, Pitágoras se dio cuenta que estos sonaban particularmente parecido, aunque uno tuviera un sonido más grave que el otro.

Octavas recién salidas del laboratorio.

En ocasiones puede parecer que el ponernos técnicos la música se vuelve algo inaccesible, para que no siga quedando con esta sensación. Podemos empezar diciendo que, como cualquier otra disciplina, la forma en la que entendemos la música dependerá del lugar y de la época en la que nos encontremos, dicho esto, es necesario aclarar que vamos a hablar de música como esta es entendida en occidente.

Imaginemos que estamos en un laboratorio, pero este es un laboratorio especial, aquí no hay batas ni lentes de laboratorio, no hay matraces ni básculas, no hay aparatos para medir. En este laboratorio sólo existe un objeto, un instrumento especial que se llama monocordio, el monocordio es un invento que Diógenes le atribuye a Pitágoras, se trata de una caja la cual tiene una cuerda atada a los extremos y una cuña debajo de ella.

El científico a cargo de este laboratorio no es otro que el personaje que nos ha acompañado durante todo este viaje, Pitágoras. Cuando Pitágoras tensó la cuerda de su monocordio y la hizo vibrar “al aire” pudo evocar un tipo de sonido, de aquí podemos preguntarnos, ¿Cómo creamos nuevos sonidos?

Recordemos que cuando Pitágoras presenció el evento donde escucho diferentes sonidos cuando los herreros golpeaban sus martillos, notó que la diferencia de estos era por el peso de estos instrumentos de trabajo, entonces él trasladó esta idea colocando la cuña a diferentes distancias de la cuerda de su monocordio de forma muy parecida en que en la actualidad “pisamos” las cuerdas de una guitarra para crear diferentes sonidos. Al igual que con los martillos, se dio cuenta que colocando la cuña justo a la mitad de la cuerda el sonido que esta emitía se parecía mucho al que daba con la cuerda “al aire” solo que un poco más aguda. De forma similar, cuando Pitágoras divide la cuerda en cuatro de forma imaginaria y colocaba la cuña de forma que de un lado hubiera ¼ de la cuerda y del otro lado de la cuña ¾ de la cuerda, al tocar la parte más corta se daba cuenta que el sonido seguía siendo parecido al tocar la cuerda al aire pero ahora mucho más aguda. Esto es lo que tiempo después conoceríamos como tocar la misma nota, pero una octava más arriba o bien más abajo.

¿Cómo se tocan otras notas?

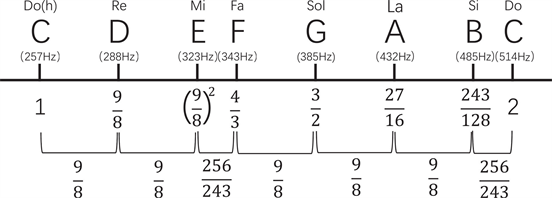
Gracias a los experimentos aprendimos que al tener una “nota” en una cuerda y al dividir el segmento que tocamos a la mitad obtenemos la misma nota una octava más arriba, pero no podemos vivir eternamente de vivir la misma nota tonos más arriba y tonos más abajo, por ello vale la pena preguntarse una forma de alcanzar otras notas musicales ¿cómo hacemos esto? Probablemente conoces las notas musicales

Do, Re, Mi, Fa, Sol, La, Si

Existe una forma más técnica de nombrarlas y esto es por tono. A esta sucesión de tonos la conocemos por el nombre de escala diatónica. Suele considerarse que la cuerda tocada al aire es Do, mientras que tocada a la mitad es Do mayor, para esté punto se estará preguntando ¿cómo se hizo para encontrar las seis notas restantes?

Pitágoras no tenía forma de medir frecuencias de sonido o características parecidas, por lo que basó su estudio en relaciones sonoras que, como decíamos al principio del texto, se trata de comparar cosas para poderlas medir. Pitágoras utilizó un sistema en el que comparaba las proporciones de las distancias en que pisaba la cuerda de su monocordio y así comparaba diferentes tonos, para esto, dividió con la cuña a la cuerda de tal forma que de un lado de esta hubiera ⅓ de la cuerda y del otro lado de la cuña los ⅔ restantes, después, hizo vibrar, ¿por qué a ⅔? ya que Pitágoras estaba obsesionado con armonizar todas las cantidades utilizó la media armónica de 1 y ½, es decir la media armónica entre Do y Do mayor.

Si se están preguntando ¿qué es una media armónica? La respuesta a esta pregunta podemos encontrarla de la mano de Bullen (2013), pues nos define la media armónica como “tomar” un par de números a y b mayores a 0 y realizar la siguiente operación.

21a+1b

Esto es, el número de cantidades (en este caso sólo tenemos dos) dividido entre la suma de los inversos multiplicativos de estas cantidades. Por lo anterior, obtenemos que la media armónica entre 1 y ½ es la siguiente.

211+112=21+2=23

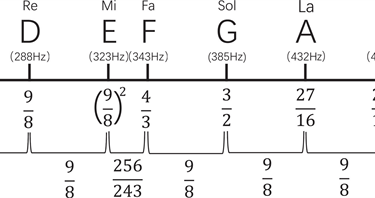
Al tono que se encuentra en relación 2:3 de otro tono le vamos a decir que es una quinta, por ejemplo el tono resultante de hacer vibrar ⅔ de la distancia a la que hacíamos vibrar Do se le llamamos Fa pues es cinco tonos más baja, por otra parte, como estamos trabajando con proporciones, el tono que esté en relación 3:2 de Do le llamamos Sol pues está cinco tonos por encima de Do

Fa, Sol, La, Si, Do

Do, Re, Mi, Fa, Sol

¿Qué significa esto?, no es otra cosa que si Pitágoras toca Do haciendo vibrar su monocordio al aire y Do una octava más abajo la toca pisando la mitad de la cuerda de su instrumento, entonces, para tocar Sol que esté entre estas dos octavas debe de hacer el siguiente cálculo.

1232=34

Entonces pisando la cuerda de su monocordio a ¾ Pitágoras estaría tocando Sol

Por otra parte, para tocar Re, sabemos que este tono lo podemos encontrar 5 tonos más arriba, es decir, hacemos el siguiente cálculo.

3432=98

Pero esta fracción al ser más grande que 1 sale de nuestro instrumento, entonces, podemos bajarlo una octava dividiéndolo entre 2.

9812=916

De la misma forma podemos encontrar a La y Mi, La está una octava arriba de Re, entonces, podemos hallar a La con la siguiente operación.

91632=2732

Mientras que a Mi lo encontramos llevando a cabo las operaciones.

273232=8164

816412=81128

la escala conformada por los tonos

Do, Re, Mi, Sol, La

Se le conoce como la escala pentatónica, la cuál es base de mucha de la música que se hacía en la antigüedad y en la actualidad, esta es una escala muy frecuente a la hora de hacer improvisación musical, utilizada mucho en géneros como la música jazz.

De forma análoga a cómo lo hemos estado haciendo, podemos encontrar los tonos de Fa y Si en las posiciones 7291024 y 243256 respectivamente.

Esta es la forma en la que Pitágoras creó la escala musical que conocemos hoy en día. A este arreglo de siete tonos dispuestos en esas proporciones le colocamos el nombre de escala diatónica, Podríamos quedarnos en este punto y hacer música únicamente con la teoría que acabamos de construir pero aún podemos hacer la pregunta ¿hay más después de esto?.

Después de la escala diatónica

Probablemente te hayas preguntado ¿por qué utilizamos esas proporciones?, ¿qué pasa si toco en posiciones distintas a los siete tonos establecidos? Aunque pueda parecer que las reglas musicales sean algo arbitrarias, el hecho es que ya ha habido personas que se han hecho estas preguntas y para esto han definido el concepto de semitono.

Si observas un piano puedes darte cuentas que este tiene teclas negras y blancas, esto es porque las teclas blancas corresponden a los tonos de la escala diatónica mientras que las teclas negras que están en medio de dos teclas blancas corresponden a lo que podemos llamar un tono intermedio como podemos observar en la siguiente imagen.

La primer tecla blanca (de izquierda a derecha de la imagen) corresponde a un Do, la primera tecla negra (de izquierda a derecha de la imagen) corresponde a un Do sostenido que se le denota como Do#, la segunda tecla blanca corresponde a un Re y la segunda tecla negra corresponde a un Re sostenido Re#. Entonces, en el piano podemos encontrar la siguiente escala.

Do, Do#, Re, Re#, Mi, Fa, Fa#, Sol, Sol#, La, La#, Si

A esta le llamamos escala cromática y podemos decir que es de alguna forma una colección más completa de tonos.

Aun así, podemos ir más lejos, ¿qué es lo que pasa entre cada tono y semitono? Existen compositores, como el mexicano Julián Carrillo, que han propuesto una nueva teoría musical como es la del sonido 13. Sonido 13 de Julián Carrillo (s.f.), que trata de ver la sucesión de tonos como un “viaje continuo”, es decir, podemos encontrar más sonidos dentro de los tonos establecidos y podemos hacer cosas interesantes con ellos. Pero este es un viaje en el que aunque ya hemos estado un par de tiempo, apenas va empezando, puede que en un par de años concibamos la música de una forma distinta, con nuevos tonos e instrumentos.

Referencias 

• Heller-Roazen, D. (2011). The Fifth Hammer: Pythagoras and the Disharmony of the World. Zone Books

• Bullen, P. (2013). Means and Their Inequalities. International Journal of Mathematics and Mathematical Sciences

• Sonido 13 de Julián Carrillo (s.f.). Sonido 13 de Julián Carrillo (entrevista a Julián Carrillo). [Video], Fuente. https://www.youtube.com/watch?v=e_vYQQ3zL0c&t=845s